Quantum calculus /

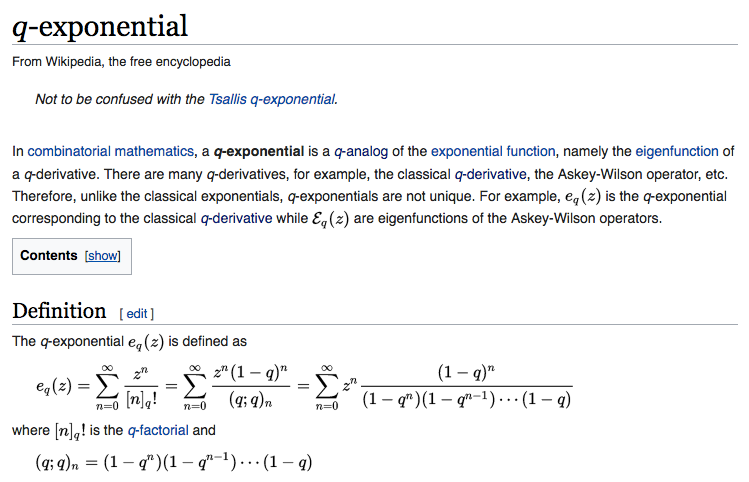
Consider any real or complex variables q, and let's take a look at the expression

1 + q + q·q + q·q·q + q·q·q·q + q·q·q·q·q which can also be written as 1 + q + q^2 + q^3 + q^4 + q^5 Read this as a function in q, i.e. consider the following polynomial, which we'll call "u6" u6(q) := 1 + q + q^2 + q^3 + q^4 + q^5

This polynomial has an important property, namely that when you plug in q=1, you find the value 6:

u6(1) := 1 + 1 + 1^2 + 1^3 + 1^4 + 1^5 = 1 + 1 + 1 + 1 + 1 + 1 = 6

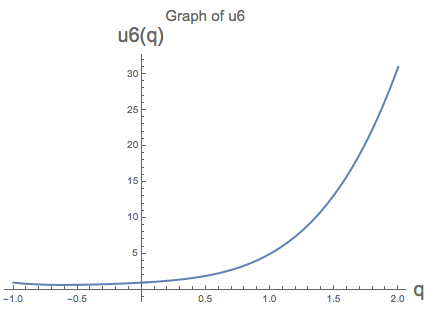
Here is the graph of the function, u6(q), with q interpreted as real number in the inteveral from -1 and 2.

For sure, if you have any non-negative integer k, then q^k at q=1 equals 1^k, which is just 1. For this reason, any polynomial that is the sum n terms of the form q^k, will, at q=1, evaluate to n. For example, consider

u8(q) := 1 + q + q^2 + q^3 + q^4 + q^5 + q^6 + q^7

If fulfulls

u8(1) := 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 8

Now, more generally, let's consider a function u(n,q) of two arguments. The first argument shall be an integer, n, and the second any other number, q.

u(n,q) := 1 + q + q^2 + q^3 + .... + q^(n-2) + q^(n-1)

As I hope I've motivated above, this function fulfulls

u(n,1) := 1 + 1 + 1^2 + 1^3 + .... + 1^(n-2) + 1^(n-1) = n

This has a surprising consequence: The arithmetic of natural numbers is embedded in the arithmetic of those functions.

For example, consider the function u(2,q) and u(3,q). Define two new functions, f and s, like so:

f(q) := u(2,q) + u(3,q)

and

s(q) := u(2,q) * u(3,q)

which means

f(q) = (1 + q) + (1 + q + q^2) = 2 + 2·q + q^2

and

s(q) = (1 + q) * (1 + q + q^2) = 1 + 2·q + 2·q^2 + q^3

Because of what's been said before, those two functions are actually just deformations of the numbers five and six. Indeed

f(1) = 2 + 2·1 + 1^2 = 5

and

s(q) = 1 + 2·1 + 2·1^2 + 1^3 = 6

We see that we can abstract away from the natural numbers and works with functions, which secretly at one point know about basic arithmetic. However, at the pint q=3.5, the u's will not look related to the natural numbers and their arithmetic is something much wilder.

The most serious application of this concept is in combinatorics of vector spaces. The subject goes by the name of q-analogs and has toy applications in various fields.

Quantum calculus /

comments