
ပထမမွန္ေျပာင္းအေၾကာင္းေရးတယ္။ မွန္ေျပာင္းနဲ႔ ၾကယ္ေလးေတြကိုၾကည့္ဖို႔၊ ေနာက္ ၾကယ္ကေလးမ်ား ကိုေရတြက္ျခင္းအေၾကာင္းေရးတယ္။အခု ၾကယ္၊ ျဂိဳဟ္၊ ကမာၻေတြဘယ္ေလာက္ၾကီးျပီး ဘယ္ေလာက္ေဝးသလဲ ဆိုတဲ့ အေၾကာင္းေရးပါမယ္။ ဒီေဆာင္းပါးက အတြက္အခ်က္မ်ားပါလို႔ စိတ္ကေလးနည္းနည္းရွည္ျပီး သည္းခံ ဖတ္ေပးေစလိုပါတယ္။
ပထမဦးဆံုး ၾကယ္၊ ျဂိဳဟ္၊ ကမာၻေတြဘယ္ေလာက္ၾကီးျပီး ဘယ္ေလာက္ေဝးသလဲ ဆိုတာကို တိုင္းတာ တြက္ခ်က္ေတာ့မယ္ဆိုေတာ့ ေပတံလိုပါျပီ။ ေပၾကိဳးလိုပါျပီ။ ကိုယ္ေတြျမင္ေတြ႔ေနက် ေပတံေတြေပၾကိဳးေတြနဲ႔ ေတာ့မရဘူးေပါ့။သူတို႔ေတြကိုတိုင္းတာမွာကိုက ဘယ္ႏွစ္ေပ၊ ဘယ္ႏွစ္ကိုက္၊ဘယ္ႏွစ္မိုင္တိုင္းမွာမဟုတ္ေတာ့ ။ေပၾကိဳးဆိုတာကလည္း အလင္းႏွစ္နဲ႔ တိုင္းတာႏိုင္တဲ့။ ေပၾကိဳးမဟုတ္တဲ့ အလင္းၾကိဳးမွ်င္ေပါ့။ အားလံုးသိၾကတဲ့ အတိုင္း ဒီေလာက္ေဝးတဲ့ေနရာေတြကို တိုင္းတာဖို႔ဆိုတာက အလင္းႏွစ္နဲ႔ပဲတိုင္းတိုင္ႏိုင္မွာပါပဲဆိုတာေလ။ ဒီေတာ့ အလင္းဟာတစ္စကၠန္႔ကို မိုင္ေပါင္း ၁၈၆၀၀၀ သြားတယ္ဆိုတာ သိမွျဖစ္ပါမယ္။ သိျပီးသားကသိျပီး သားလို႔ မွတ္ျပီးမသိေသးသူက သိရျပီလို႔မွတ္ပါေလ။
တစ္စကၠန္႔ကို မိုင္ေပါင္း ၁၈၆၀၀၀ သြားတဲ့အလင္းဟာ တစ္ႏွစ္မွာ ဘယ္ေလာက္သြားမလဲ။တစ္ႏွစ္မွာ ရွိတဲ့ စကၠန္႔ေပါင္းက ၃၆၅(ရက္) x ၂၄(နာရီ) x ၆၀(မိနစ္) x ၆၀(စကၠန္႔) = ၃၁,၅၃၆,၀၀၀ စကၠန္႔ရွိပါတယ္။ ဒါကို တစ္ႏွစ္မွာ အလင္းသြား မယ့္အကြာ အေဝးကိုတြက္ေတာ့ ၃၁,၅၃၆,၀၀၀ x ၁၈၆,၀၀၀ = ၅,၈၆၅,၆၉၆ x ၁၀၆ မိုင္ျဖစ္ပါတယ္။ဒီေတာ့ ၾကယ္၊ ျဂိဳဟ္၊ ကမာၻေတြဘယ္ေလာက္ၾကီးျပီး ဘယ္ေလာက္ေဝးသလဲတြက္ဖို႔ အလင္းရဲ့ တစ္ႏွစ္သြားမယ့္ မိုင္အကြာ အေဝးေတာ့သိရပါျပီ။ ေနာက္တစ္ခုက အလင္းအားကိုသိဖို႔လိုျပန္ပါေသးတယ္။ေနရဲ့ အလင္းအားကေတာ့ 38 x 10^27 candle power ရွိတယ္ဆိုေတာ့ ေနရဲ့ အလင္းအားကိုပဲအေျခခံျပီး တြက္ခ်က္သြားလို႔ရႏိုင္ပါျပီ။
ဟီးဟီး နည္းနည္းမ်ားသလိုပဲေနာ္၊ မွန္ေျပာင္းတစ္လက္ေတာင္မဝင္ႏိုင္နဲ႔သူက ၾကီးၾကီးက်ယ္က်ယ္ ၾကယ္၊ ျဂိဳဟ္၊ ကမာၻေတြဘယ္ေလာက္ၾကီးျပီး ဘယ္ေလာက္ေဝးသလဲဆိုတာတြက္မလို႔ဆိုပဲေလ။ခုေတာ့ ဘာပဲျဖစ္ျဖစ္စခဲ့ ျပီဆိုေတာ့ တြက္ရေတာ့မွာပါ။ တြက္နည္းကေတာ့ ကၽြန္ေတာ္တို႔ ၉ တန္း ၁၀ တန္းမွာသင္ခဲ့ရတဲ့ ပိုက္သာဂိုးရပ္သီအိုရမ္တို႔၊ Sine ,Cosine တို႔မွတ္မိၾကေသးတယ္မို႔လားလား။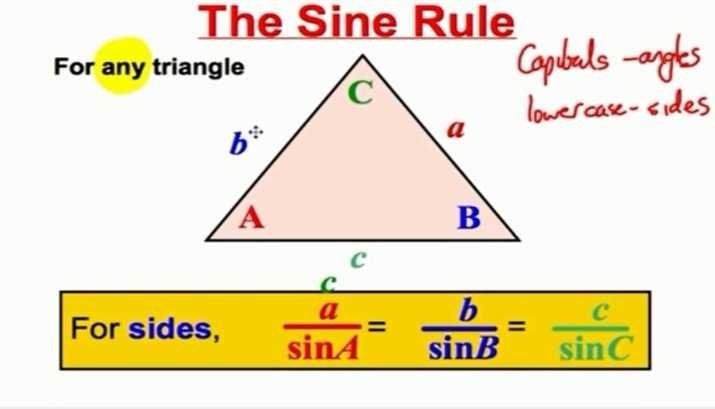
Sine Rule
A sina β = B sine ã
ၾတိဂံတစ္ခုရဲ့ အနားတစ္ဖက္အရွည္ရယ္။ အဲဒီၾတိဂံရဲ့ ေထာင့္သံုးဖက္ရယ္ကို သိရင္ က်န္တဲ့အနားေတြရဲ့ အရွည္ေတြလည္းသိျပီဆိုေတာ့ ပထမဆံုးဒီလိုစဥ္းစားၾကည့္ရေအာင္ ….
အခု အနီးအနားက ooredoo တာဝါတိုင္တို႔၊ Telenor တာဝါတိုင္တို႔၊MPT တာဝါတိုင္တို႔ရဲ့ အျမင့္ေတြကို စမ္းျပီးတိုင္းၾကည့္ရေအာင္
ooredoo တာဝါတိုင္ေအာက္ေျခကေန ေပ ၂၀၀ အကြာေနရာမွာ အမွတ္တစ္ခုထားျပီး အဲဒီအမွတ္ကေန ooredoo တာဝါတိုင္ထိပ္ကို လွမ္းၾကည့္လိုက္တဲ့အခါ ေျမျပင္ကေန ၈၅ ဒီဂရီ အေစာင္းရွိတယ္ဆိုပါစို႔။ ဒါဆိုရင္ ေဒါင့္ေတြက ၈၅ံ၊၁၅ံ၊၉၀ံ အသီးသီးရပါမယ္။
Sine Rule အရ
A sin β = B sin ã
A sin 15 ံ = 200 sin 85 ံ ျဖစ္ေတာ့
sin 15 =0.2588190451
sin 85 = 0.9961946809
A= 200 x 0.9961946809 †0.2588190451
A= 769.8 ft ျဖစ္တဲ့အတြက္ ooredoo တာဝါတိုင္ဟာ 769.8 ft ျမင့္တယ္လို႔ အဓိပၸါယ္ထြက္ပါတယ္။ အတိုင္းအတာမ်ားက စိတ္မွန္းျဖစ္တဲ့အတြက္ အတိအက်ယူလို႔ေတာ့မရပါဘူး။ အတိအက်သိခ်င္ရင္ေတာ့ တိုင္ နားကိုသြားျပီးဒီနည္းအတိုင္းတိုင္းလို႔ရပါတယ္။ေဒါင့္ေတြပဲမွန္ဖို႔လိုပါတယ္။ေဒါင့္မွန္ရင္အျမင့္လည္းမွန္ပါျပီ။ ေအာက္ေျခကြာအေဝးကေတာ့ ေပၾကိဳးဆြဲမွာဆိုေတာ့ မွားဖို႔မလြယ္ပါဘူး။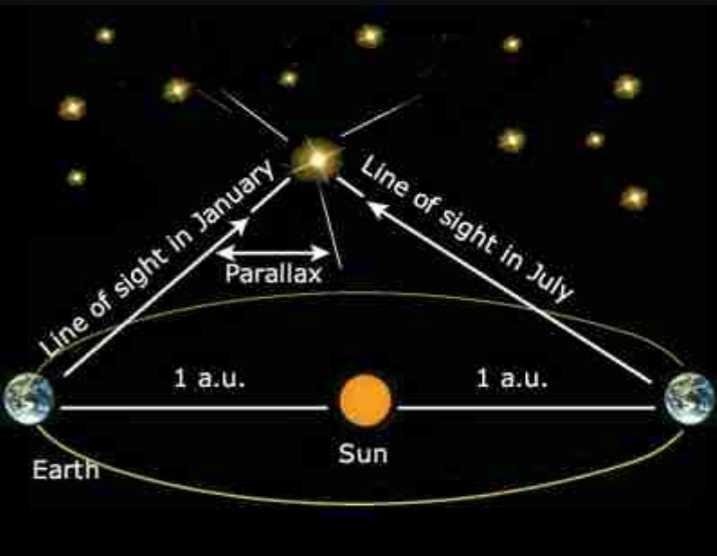
နားလည္ျပီဆိုရင္ေတာ့ ...
ပထမဦးဆံုးျဂိဳဟ္တစ္ခုကို တိုင္းဖို႔လုပ္ရပါမယ္။ ဒါကေတာ့ ေအာက္ေျခအနားကို ေပ ၂၀၀ လုပ္လို႔ မရ ေတာ့ပါဘူး။ အနည္းဆံုးရန္ကုန္နဲ႔ ျမစ္ၾကီးနားေလာက္ထားရပါမယ္။ ရန္ကုန္မွာ နကၡတ္တာရာစခန္းတစ္ခု၊ ျမစ္ၾကီး နားမွာ နကၡတ္တာရာစခန္းတစ္ခု ဒီစခန္း ၂ ခုရဲ့ အေျဖာင့္အတိုင္း အကြာအေဝးကို အရင္သိေအာင္လုပ္ရပါမယ္။ သိျပီဆိုရင္ေတာ့ အဲဒီစခန္းေတြကေန ကိုယ္အကြာအေဝးတိုင္းမယ့္ျဂိဳဟ္ကို ေရြးခ်ယ္သတ္မွတ္ျပီး စခန္းႏွစ္ခုရဲ့ အေျဖာင့္မ်ဥ္းကေန ကိုယ္သတ္မွတ္ထားတဲ့ျဂိဳဟ္ကို ဘယ္ေလာက္ေဒါင့္မွာ ျမင္ရတာလဲဆိုတာကို တိုင္းတာ ရပါမယ္။ေဒါင့္ ၂ ခုရျပီဆိုရင္ က်န္ေဒါင့္ကလည္း အလိုလိုရျပီေလ။ ရရင္ ေစာေစာကတြက္နည္း အတိုင္း တြက္လိုက္ရင္ အေျဖထြက္ပါျပီ။
မင္းစိုးႏိုင္
MSC-010
Photo – Google
Posted using Partiko Android