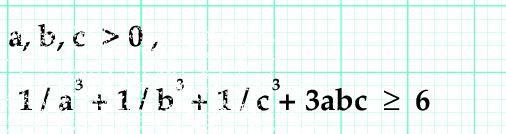a, b, c > 0
Demostrar
1/a³ + 1/b³ + 1/c³ + 3abc ≥ 6
Tenemos una desigualdad en la que intervienen funciones simétricas,
las terceras potencias sobre los valores recíprocos .
Podemos establecer una relación entre los valores, α , y sus recíprocos, 1/α , vía las funciones simétricas unitarias , en .
x ³ − e1 x ² + e2 x − e3 = 0
Construimos la ecuación con soluciones recíprocas,
y ³ − ( e2 / e3 ) y ² + ( e1 / e3 ) y − (1 / e3 ) = 0
Conocido el valor de las funciones simétricas podemos determinar el valor de las sumas de las terceras potencias , ∑1/p³ , mediante las identidades de Newton.
3 e3² − 3 e1 e2 e3 + e2³
∑1/p³ = ――――――――――――
e3³
Podemos expresar la desigualdad original como,
∑1/p³ + 3 e3 ≥ 6
3 e3² − 3 e1 e2 e3 + e2³
―――――――――――― + 3 e3 ≥ 6
e3³
La siguiente desigualdad entre las funciones simétricas unitarias ,
nos permite resolver el problema, expresando e1 y e2 en función de e3 ,
e1 ≥ 3 e31 / 3
e2 ≥ 3 e32 / 3
Sustituyendo y simplificando,
e3 + 1 / e3 ≥ 2
Hemos transformado el problema original en una desigualdad que puede verificarse empleando las propiedades de las medias aritmética/geométrica, que es evidentemente cierta, de forma que queda demostrada la validez de la desigualdad bajo estudio.
∎